Problems tagged with "maximum likelihood"

Suppose a discrete random variable \(X\) takes on values of either 0 or 1 and has the distribution:

where \(\theta\in[0, 1]\) is a parameter.

Given a data set \(x_1, \ldots, x_n\), what is the maximum likelihood estimate for the parameter \(\theta\)? Show your work.

Suppose data points \(\nvec{x}{1}, \ldots, \nvec{x}{n}\) are drawn from an arbitrary, unknown distribution with density \(f\).

True or False: it is guaranteed that, given enough data (that is, \(n\) large enough), a Gaussian fit to the data using the method of maximum likelihood will approximate the true underlying density \(f\) arbitrarily closely.

Suppose a Gaussian with a diagonal covariance matrix is fit to 200 points in \(\mathbb R^4\) using the maximum likelihood estimators. How many parameters are estimated? Count each entry of \(\mu\) and the covariance matrix that must be estimated as its own parameter.

8 Show Answer

Suppose a continuous random variable \(X\) has the density:

where \(\theta\in(0, \infty)\) is a parameter, and where \(x > 0\).

Given a data set \(x_1, \ldots, x_n\), what is the maximum likelihood estimate for the parameter \(\theta\)? Show your work.

Suppose a Gaussian with a diagonal covariance matrix is fit to 200 points in \(\mathbb R^4\) using the maximum likelihood estimators. How many parameters are estimated? Count each entry of \(\vec\mu\) and the covariance matrix that must be estimated as its own parameter (the off-diagonal elements of the covariance are zero, and shouldn't be included in your count).

8 Show Answer

Suppose a univariate Gaussian density function \(\hat f\) is fit to a set of data using the method of maximum likelihood estimation (MLE).

True or False: \(\hat f\) must be between 0 and 1 everywhere. That is, it must be the case that for every \(x \in\mathbb R\), \(0 < \hat f(x) \leq 1\).

Consider Justin's rectangle density. It is a parametric density with two parameters, \(\alpha\) and \(\beta\), and pdf:

A picture of the density is shown below for convenience:

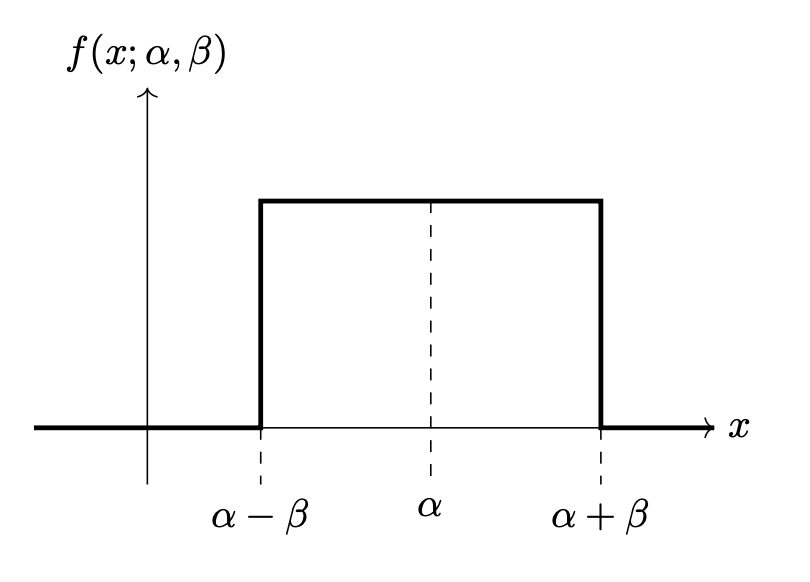
In all of the below parts, let \(\mathcal X = \{1, 2, 3, 6, 9\}\) be a data set of 5 points generated from the rectangle density.

Your answers to the below problems should all be in the form of a number. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.

Consider the following set of 6 data points:

In the below parts, your answers should be given as numbers. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.

Consider the following set of 6 data points:

In the below parts, your answers should be given as numbers. You may leave your answer as an unsimplified fraction or a decimal, if you prefer.

Suppose it is known that the distribution of a random variable \(X\) has a univariate Gaussian density function \(f\).

True or False: \(f\) must be between 0 and 1 everywhere. That is, it must be the case that for every \(x \in\mathbb R\), \(0 < f(x) \leq 1\).